高考中數(shù)列是較難的部分嗎?如何選擇合適的數(shù)學補習班?
在高考數(shù)學中較后幾道題目基本上都是以大題的形式呈現(xiàn)的,比如說數(shù)列或者是函數(shù)再者是幾何問題等等,那么在這些大題中較難的是數(shù)列嗎?高考中數(shù)列的難度是怎樣的呢?想要補習高中數(shù)學的內(nèi)容,學生應該如何選擇補習班呢?在眾多的補習班中伊頓教育數(shù)學補習班是怎樣的呢?下面秦學小編就來帶領學生們學習關于高考數(shù)列的相關內(nèi)容以及高中數(shù)學輔導班的選擇問題,希望學生們在數(shù)學方面成績有所沖刺。

客觀來說,目前為止數(shù)列在高考中還不算是較難的題目。至于今后有沒有可能成為較難的,這個并不是較重要的,重要的是要根據(jù)考綱要求來做好備考準備,另外就是不斷在解題的過程中增強讀題能力、理解能力和計算力。
現(xiàn)在高考的主要難點暫時還停留在導數(shù)以及概率分布列還有圓錐曲線中,對于數(shù)列暫時還不會考這么難,因此短期內(nèi)這種形式的數(shù)列大題在高考中一般不會出現(xiàn)。但仔細看來,這道大題蘊含了多關于數(shù)列的考點,同學們可以把這道例題當作一個重要的數(shù)列知識點來研讀。
深度解析過程
1、讀題分析
從題目結(jié)構(gòu)以及條件來看,本題主要涉及了如下的幾個考點:
①等差等比通項公式的求解
②分段數(shù)列的通項討論
③數(shù)列分組求和的應用與書寫規(guī)范
④錯位相減求和的應用
⑤數(shù)列前n項積的處理以及分離參數(shù)的使用
從上述的分析結(jié)果可知:本題確實是一道綜合且具有很高難度的數(shù)列大題,各位同學應該細心琢磨,帶著查缺補漏弄清知識點的心態(tài)去研究。
總體來說,這道題算得上是一道綜合且有難度的數(shù)列大題:
①首先,本題的第一問是計算等差數(shù)列與等比數(shù)列通項公式的問題,求解此類問題請同學們記住將等差數(shù)列與等比數(shù)列的項分別用“首項+公差”以及“首項×公比”的形式表達出來。并注意消元計算。
②其次,本題的第二問涉及到了n奇偶性的討論,應對這類問題我們通常都是將需要分類討論的數(shù)列多寫幾項出來,這樣更能準確無誤地看清數(shù)列的規(guī)律,從而更好地分類討論,此外在使用分組求和法對數(shù)列進行求和時,我們較好設出An與Bn這樣的子數(shù)列,這樣求和的時候能夠更有章法!
③第三,要注意在使用錯位相減法對數(shù)列求和時,要對數(shù)列的“指數(shù)部分”進行化簡,這樣能更好地看出公比。
④較后,應對數(shù)列前n項積問題的時候,我們通常可以采取的辦法是:寫出數(shù)列的前一項,然后將其與原數(shù)列相除,這樣便可以抵消掉很多的項,較后如果相除的結(jié)果大于1,那么此數(shù)列遞增,反之亦然!
寫在文末
目前為止數(shù)列不可能考察出很難的題目,但是強化數(shù)列解題思維本身也沒有錯,至少可以預防遇到類似上述這道數(shù)列難題。此外,數(shù)列的難題再難,它也有章法,一道數(shù)學題都是一樣。
題目的難與簡單是因人而異的,關于更多的數(shù)學補習班的內(nèi)容同學們可以關注伊頓教育,來看看吧。

- 學業(yè)水平系統(tǒng)測評
- 個性化針對教學計劃
- 線下逆襲試聽課
- 系列學科學習資料




- 熱門課程
- 熱門資訊
- 熱門資料
- 熱門福利
-
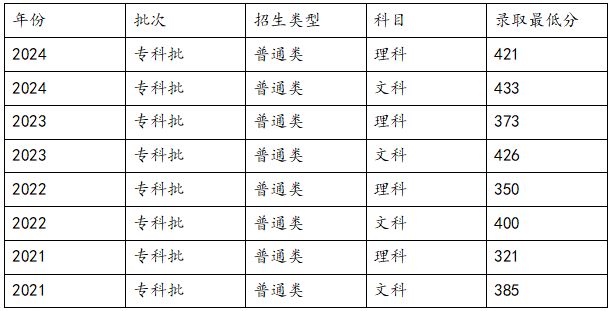 高考301分想沖刺陜工院?歷年錄取分數(shù)多少?【摘要】高考成績出來了,考了301分,孩子心里想著陜西工業(yè)職業(yè)技術學院,又緊張又期待,陜工院是國家“雙高計劃”A檔建設院校,實力很強,好多考生都想去。這時候,陜工院歷年的錄取分數(shù)就很關鍵了,能知道自己有沒有希望考上,一定要來了解一下歷年的錄取分數(shù)線。
高考301分想沖刺陜工院?歷年錄取分數(shù)多少?【摘要】高考成績出來了,考了301分,孩子心里想著陜西工業(yè)職業(yè)技術學院,又緊張又期待,陜工院是國家“雙高計劃”A檔建設院校,實力很強,好多考生都想去。這時候,陜工院歷年的錄取分數(shù)就很關鍵了,能知道自己有沒有希望考上,一定要來了解一下歷年的錄取分數(shù)線。 -
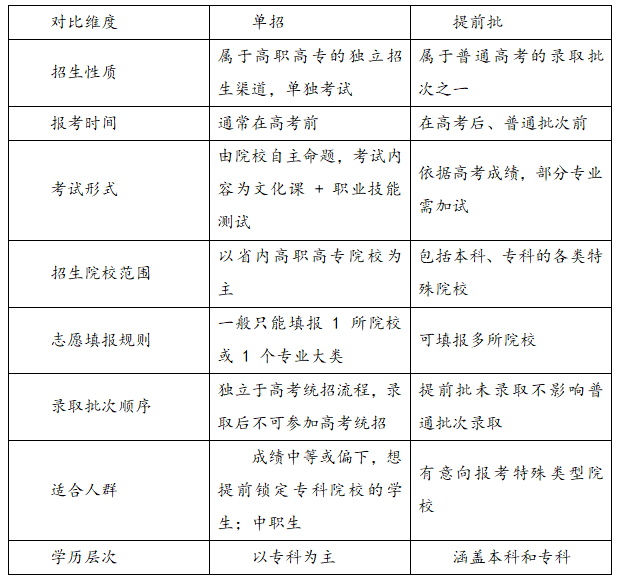 單招和提前批是什么意思?有哪些區(qū)別?一、單招和提前批是啥意思? 單招就是單獨招生,全名叫“普通高等職業(yè)教育單獨考試招生”。就是高等職業(yè)院校自己出題、自己組織考試、自己決定錄取誰,主要招中等職業(yè)學校的學生和普通高中畢業(yè)生。考試一般考文化課和職業(yè)技能。考上以后,和高考統(tǒng)招的學生待遇一樣。 提前批是普通高考招生里的一個錄取批次,在普
單招和提前批是什么意思?有哪些區(qū)別?一、單招和提前批是啥意思? 單招就是單獨招生,全名叫“普通高等職業(yè)教育單獨考試招生”。就是高等職業(yè)院校自己出題、自己組織考試、自己決定錄取誰,主要招中等職業(yè)學校的學生和普通高中畢業(yè)生。考試一般考文化課和職業(yè)技能。考上以后,和高考統(tǒng)招的學生待遇一樣。 提前批是普通高考招生里的一個錄取批次,在普 -
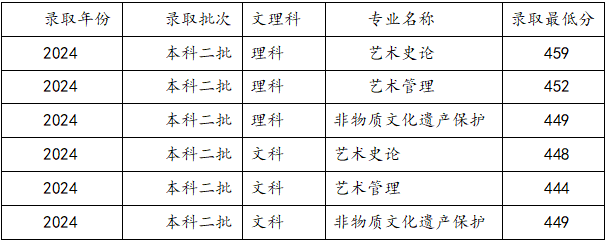 藝考音樂類包括什么專業(yè)及就業(yè)方向?西安音樂學院錄取分數(shù)【摘要】好多懷揣藝術夢想的學生都想走音樂藝考這條路,但是選啥專業(yè)對以后發(fā)展影響挺大的,考學校的話,錄取分數(shù)可是個關鍵門檻。今天咱就嘮嘮藝考音樂類有啥專業(yè),能干啥工作,還有西安音樂學院的錄取分數(shù)是多少,讓大家心里有數(shù),在學音樂的路上走得穩(wěn)當點。
藝考音樂類包括什么專業(yè)及就業(yè)方向?西安音樂學院錄取分數(shù)【摘要】好多懷揣藝術夢想的學生都想走音樂藝考這條路,但是選啥專業(yè)對以后發(fā)展影響挺大的,考學校的話,錄取分數(shù)可是個關鍵門檻。今天咱就嘮嘮藝考音樂類有啥專業(yè),能干啥工作,還有西安音樂學院的錄取分數(shù)是多少,讓大家心里有數(shù),在學音樂的路上走得穩(wěn)當點。 -
 單招寄宿制學校靠譜嗎?西安博大教育環(huán)境咋樣?【摘要】現(xiàn)在升學競爭越來越激烈,好多學生想通過單招實現(xiàn)上學的夢想,單招寄宿制學校就受到許多家長的關注了。那些特別想讓孩子通過單招上理想學校的家長和學生,最關心的就是這種學校靠不靠譜,能不能幫孩子實現(xiàn)夢想,在西安的教育機構(gòu)里,西安博大教育挺受關注的,大家都想知道它的環(huán)境怎么樣。本期就跟隨小編一起看看吧!
單招寄宿制學校靠譜嗎?西安博大教育環(huán)境咋樣?【摘要】現(xiàn)在升學競爭越來越激烈,好多學生想通過單招實現(xiàn)上學的夢想,單招寄宿制學校就受到許多家長的關注了。那些特別想讓孩子通過單招上理想學校的家長和學生,最關心的就是這種學校靠不靠譜,能不能幫孩子實現(xiàn)夢想,在西安的教育機構(gòu)里,西安博大教育挺受關注的,大家都想知道它的環(huán)境怎么樣。本期就跟隨小編一起看看吧!
-
 高考作文素材積累:流浪詩人——我的人生之路各位學生注意了,現(xiàn)在就要進入到2023年陰歷新年,各位學生過完年距離中高考又進了一步,為方便大家能夠積累更多的作文素材,小編老師為定期為大家更新優(yōu)秀范文,下面大家一起來賞析“流浪詩人——我的人生之路”。 作文題 閱讀下面的材料,根據(jù)要求寫一篇不少于800字的文章。(60分) 黃大發(fā),一位普
高考作文素材積累:流浪詩人——我的人生之路各位學生注意了,現(xiàn)在就要進入到2023年陰歷新年,各位學生過完年距離中高考又進了一步,為方便大家能夠積累更多的作文素材,小編老師為定期為大家更新優(yōu)秀范文,下面大家一起來賞析“流浪詩人——我的人生之路”。 作文題 閱讀下面的材料,根據(jù)要求寫一篇不少于800字的文章。(60分) 黃大發(fā),一位普 -
 2023年高考作文素材積累:“絕品即常品”各位學生大家覺得高考作文多少分才過關呢?小編老師覺得作文滿分60分大家作文在56分以上才算是過關,大家都知道高考一分之差差之千里,大家不要放過任何一個可以提分的可能!為幫助大家積累素材,小編老師為大家整理了比較好的作文題目和作文范文,供大家參考! 作文題 閱讀下面的材料,根據(jù)要求寫一篇不
2023年高考作文素材積累:“絕品即常品”各位學生大家覺得高考作文多少分才過關呢?小編老師覺得作文滿分60分大家作文在56分以上才算是過關,大家都知道高考一分之差差之千里,大家不要放過任何一個可以提分的可能!為幫助大家積累素材,小編老師為大家整理了比較好的作文題目和作文范文,供大家參考! 作文題 閱讀下面的材料,根據(jù)要求寫一篇不 -
 高考英語素材,高考英語作文開頭常用句子高考英語素材,高考英語作文開頭常用句子!一提到英文寫作,很多同學就頭疼,如何組織語言、如何下筆呢?但自從知道了一些萬能的“套話”你就會發(fā)現(xiàn)自己的寫作水平會更上一層樓!下面小編老師為大家整理了高考英語作文開頭常用句子,想要了解的學生收藏起來! 開頭常用句子 1.Depending on per
高考英語素材,高考英語作文開頭常用句子高考英語素材,高考英語作文開頭常用句子!一提到英文寫作,很多同學就頭疼,如何組織語言、如何下筆呢?但自從知道了一些萬能的“套話”你就會發(fā)現(xiàn)自己的寫作水平會更上一層樓!下面小編老師為大家整理了高考英語作文開頭常用句子,想要了解的學生收藏起來! 開頭常用句子 1.Depending on per -
 西安高三化學輔導班哪家好?化學現(xiàn)在在新高考的分量也比較重,很多專業(yè)都要求選擇化學這門課。與物理相比化學不算難。最近有學生問老師西安高三化學輔導班哪家好?下面,小編老師為大家推薦西安一家比較好的高中補習機構(gòu),大家了解一下: 伊頓教育高三·化學輔導 基礎 1.激發(fā)學習動機2.培養(yǎng)學習興趣3.化學方程式總結(jié)歸納
西安高三化學輔導班哪家好?化學現(xiàn)在在新高考的分量也比較重,很多專業(yè)都要求選擇化學這門課。與物理相比化學不算難。最近有學生問老師西安高三化學輔導班哪家好?下面,小編老師為大家推薦西安一家比較好的高中補習機構(gòu),大家了解一下: 伊頓教育高三·化學輔導 基礎 1.激發(fā)學習動機2.培養(yǎng)學習興趣3.化學方程式總結(jié)歸納















 All right reserved
All right reserved
